材料的强度与破坏理论是研究材料在各种应力下的屈服或破坏的规律,本期为大家介绍那些经典的断裂准则。

岩石开裂
最大正应力准则,也称为第一强度理论或最大拉应力理论。
400多年以前,伽利略(Galileo: 1564-1642)在研究砖、铸铁和石头的拉伸断裂时,发现当施加应力达到一临界值时材料发生断裂,于是就产生了第一强度理论。
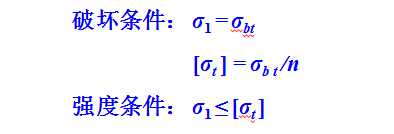
第一强度理论认为材料发生断裂是由最大拉应力引起,即最大拉应力达到某一极限值时材料发生断裂。看完第一强度理论的定义,大家可能会发现,第一强度理论适用于拉伸状态材料的破坏,第一强度理论不适用于三向压缩状态。
莫尔-库仑(Mohr-Coulomb)准则,也称为第二强度理论或最大拉应变理论。
库仑(1737-1806)在研究土和砂岩的压缩强度后,于1773年提出:当材料的破坏沿着一定剪切平面进行时,所需的破坏力不但与剪切力有关,也与剪切面上的法向力有关。
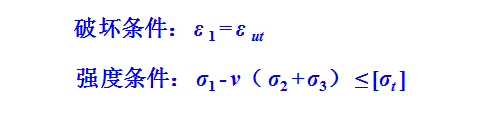
1900年德国科学家莫尔(1835-1918)将最大主应力莫尔圆引入到库仑强度理论中,因而这个破坏准则现在被称为莫尔-库仑准则。
屈特加(Tresca)准则,又称为第三强度理论或最大剪应力理论。
1864年,屈特加提出了最大剪切应力准则或称屈特加准则。当最大剪应力达到材料所固有的某一定数值时,材料开始屈服(进入塑性变形阶段),也就是说当变形体或质点中的最大切应力达到某一定值时,材料就发生屈服。
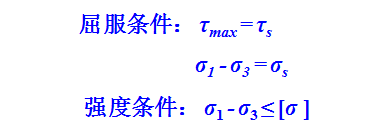
或者说,材料处于塑性状态时,其最大切应力是一个不变的定值,该定值只取决于材料在变形条件下的性质,而与应力状态无关,所以Tresca屈服准则又称为最大切应力不变条件。
Tresca屈服准则不足之处就是不包含中间主应力,没有反映中间主应力对材料屈服的影响。
范·米塞斯(van·Mises)准则,又称为第四强度理论或最大形状改变比能理论。
1913年,范·米塞斯考虑了变形能的作用,提出材料的屈服条件为其变形能达到某一临界值,此即范·米塞斯准则或第四强度理论。
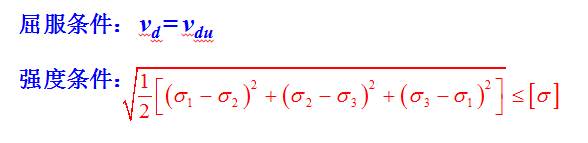
其表述是材料发生屈服是畸变能密度引起的,形状改变能密度是引起材料屈服的因素,也即认为不论处于什么样的应力状态下,只要构件内一点处的形状改变能密度达到了材料的极限值,该点处的材料就发生塑性屈服。
统一断裂准则,也称为椭圆断裂准则。
2003年前后,张哲峰研究员提出了材料的统一拉伸断裂准则。将经典的最大正应力准则、屈特加准则、范-米塞斯准则和莫尔-库仑准则有机地统一起来。
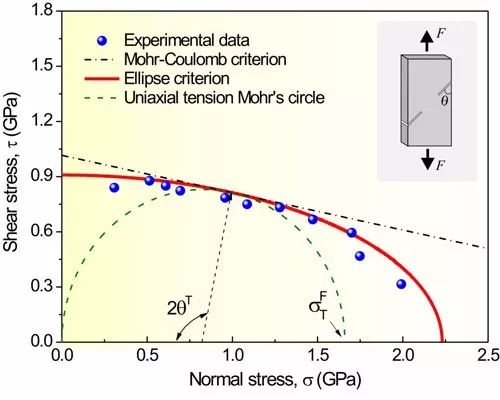
金属玻璃拉伸断裂的正应力效应和统一断裂准则的实验验证
在该统一断裂准则中,他认为脆性材料的拉伸破坏或者以剪切方式,或者以正断方式,因而存在两个临界应力τ0和σ0,其中τ0是在剪切面上无正应力时的临界剪切断裂强度,而σ0是在拉伸正断面上无剪切应力时的临界断裂强度。同时他定义了一个新的参数α=τ0/σ0为材料的断裂方式因子,它是材料的特有属性,并能控制材料剪切断裂角的大小。
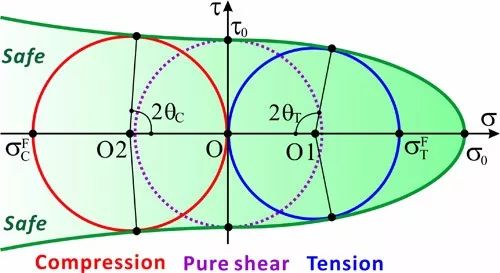
统一断裂准则及其对金属玻璃拉伸、压缩及纯剪切断裂行为的描述
当α=τ0/σ0->0时,材料的剪切断裂角接近45度,该统一准则与屈特加准则一致,也与描述单晶体屈服的施密特定律一致。
当0<α=τ0/σ0<2-1/2时,该统一准则与莫尔-库仑准则和范·米塞斯准则是一致的;同时他发现大多数金属玻璃材料的断裂方式因子范围为:1/3<α=τ0/σ0<2/3,致使其拉伸剪切断裂通常发生在50-65度角范围,并且具有高强度和比较小的拉伸-压缩断裂强度的不对称性。
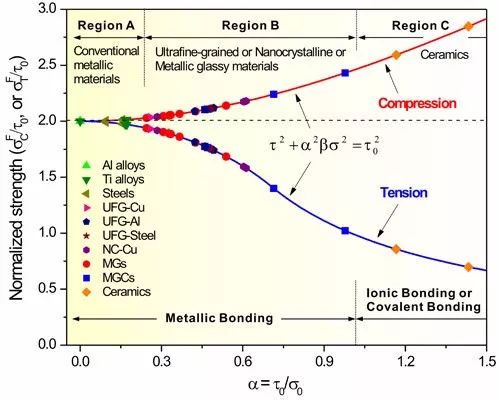
统一断裂准则对多种材料的拉伸-压缩强度不对称行为的统一描述
当α=τ0/σ0>=2-1/2时,该统一准则预测材料的破坏形式为拉伸正断,这与最大正应力准则是一致的,同时也能合理地解释其他脆性材料严重的拉伸-压缩断裂强度的不对称性。
从某种意义上讲,上述四个经典的断裂准则可以分别看作是该统一断裂准则在某一种极端条件下的特殊形式,这为揭示各种不同性能材料的普遍破坏规律提供了新的参考判据。