
1 引 言
扫描电化学显微镜(Scanning electrochemistry microscopy,SECM)是一种基于超微电极的扫描微探针电化学技术,是基于 70 年代末超微电极(Ultramicroelectrode,UME)和 80 年代初扫描隧道显微镜(Scanning Tunneling Microscopy,STM)发展起来的具有一定空间分辨率(介于普通光学显微镜和 STM)的电化学原位检测方法,其核心是电化学和原位检测。SECM 的检测信号是电流或者电位,因而具有化学反应物质灵敏性,既而不但可以研究探头或者基底电极上的异相反应电荷转移动力学和溶液中的均相反应动力学,甚至界面双电层信息,还可以原位分辨表面微区电化学不均匀性,可以弥补扫描电镜等不能直接提供电化学活性信息的不足,这对于腐蚀研究具有重要的意义。因超微电极的尺寸通常是 10 微米 μμmm,与一般扩散层的厚度具有可比性,其扩散模式与传统宏观平板电极(Planar electrode)的一维扩散模式不同,需要考虑空间三维球形扩散,导致不能简单通过 Laplace变换解 Fick 第二定律而解出电流表达式,需要计算机进行数值分析。SECM 的基本构成包含探针(即超微电极)和基底双工作电极(基底电极是否接上双恒电位仪取决于研究目的),两者的距离一般是微米级,甚至几百纳米级,导致两者的扩散场互相重叠,超微电极的电流响应不仅与溶液中氧化还原性物种浓度、扩散系数、反应动力学和超微电极半径有关,也与超微电极与基底的空间几何结构(特别是距离)有关。这就要求 SECM 实验精确控制探针与基底电极距离,并明确其大小,否则所测试电流很难获得科学解释。
SECM 在腐蚀中的应用日益受到重视。通常腐蚀研究体系中探针与基底电极距离通过测试逼近曲线,再根据理论完全正反馈或者负反馈曲线获得距离。实际上,移动探针的步进马达或者压电陶瓷移动距离与真实移动距离不完全一致,且在腐蚀研究体系中,逼近曲线也不全是完全正反馈或者负反馈响应。因此距离控制对于 SECM 在腐蚀研究中的应用是基本前提。本文结合 COMSOL 多物理场软件,构建空间二维模型,量化逼近曲线,明确基底电极反应动力学对逼近曲线的影响和步进马达移动距离与真实移动距离的关系,继而探讨了铝合金表面逼近曲线行为和真实距离控制对于 EC(电化学-化学耦合反应,如腐蚀反应中的电荷转移和腐蚀产物生成)反应动力学的影响。
2 实验方法
2.1 SECM 实验
SECM 测试采用 CHI920C 扫描电化学工作站系统,包含双恒电位仪和三维控制系统(步进马达和压电陶瓷),软件版本为 CHI Version 15.08。SECM 测试采用四电极系统,直径为 10μm 的 Pt 超微电极探针为工作电极,4 cm 长直径为 1mm 的 Pt 丝为对电极,Ag/AgCl(KCl 浓度为 3 mol/L,相对于标准氢电极电位为 0.194V)为参比电极,直径为 2 mm 的 Pt 电极为第二工作电极。
ZL104 铝合金加工成 Φ8mm×6 mm 的圆柱状,周围用聚四氟乙烯包封,保留 0.502 cm2 的端面暴露面积。实验前将铝合金表面依次用 400#、600#和 800#的水相砂纸打磨,然后用 2.5μm 的 Al2O3 抛光膏抛光至镜面,二次蒸馏水清洗,丙酮超声出油,冷风吹干。一种样品直接作为 SECM 基底电极使用,另外一种放置干燥器中 24h,以便在自然空气中形成稳定氧化膜后再进行测试。
SECM 使用中的探针和基底工作电极采用 0.3μmAl2O3 抛光膏抛光至镜面,使用 800#砂纸将 10μm的 Pt 探针的 RG(玻璃与 Pt 丝半径比)通过 800#砂纸打磨至 3,并结合光学显微镜观察确认。Pt 探针的 CV 曲线测试范围为 0~0.45V,扫速为 20mV/s。逼近曲线测试时探针电位为 0.45V,基底电极电位为0V,氧化还原电对为 0.001 mol/L 的二茂铁甲醇(Ferrocenemethanol,FcMeOH)的水溶液,支持电解质为 0.1 mol/L 的 KNO3 溶液。逼近曲线的探针逼近速率为 0.6μm/s。真实距离是根据指定位置探针 CV曲线的稳态氧化电流(iT)与远离基底时的稳态电流(iT,∞)比值,结合 COMSOL(软件许可证号:9402256)理论模拟结果获得。
2.2SECM 实验的 COMSOL 模拟模型和理论
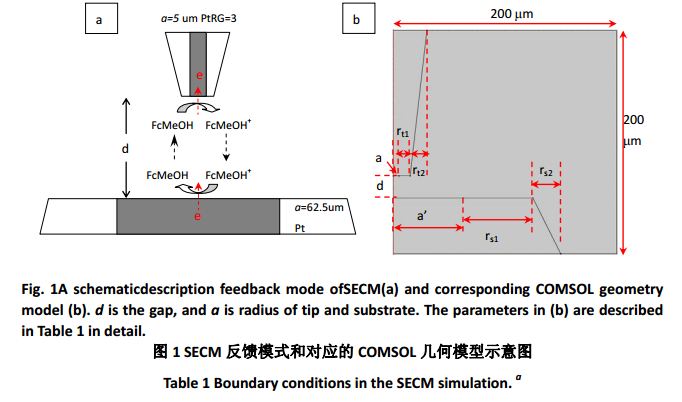
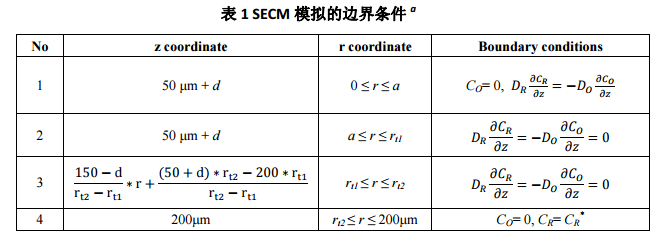
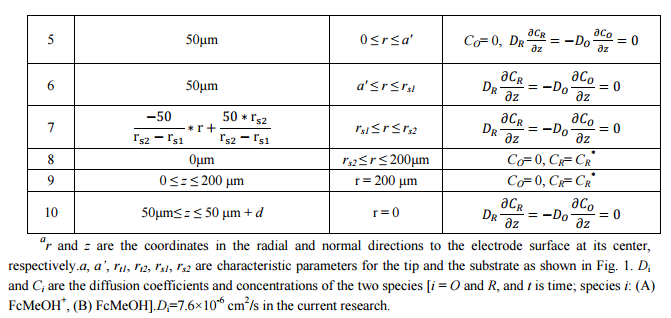
本文探针与基底电极距离的确定是根据 SECM 反馈电流并结合 COMSOL 模拟实现,如图 1a 所示。探针施加 0.45V 电位,FcMeOH 在探针上氧化处于扩散控制,基底电极的电位为 0V,FeMeOH+的还原也处于扩散控制。此时探针电流除了与电极半径和 FcMeOH 浓度有关,也与探针与基底电极距离有关。根据反馈曲线和 SECM 实验的本质电化学特征,构建如图 1b 所示的空间二维轴对称模型,其中图 1a为 SECM 的反馈模式示意图,探针施加 0.45 V 电位,氧化 FcMeOH 至 FcMeOH+,并处于扩散控制,同时基底 Pt 电极施加 0 V 电位,还原 FcMeOH+至 FcMeOH,也处于扩散控制。对应的 COMSOL 模拟的二维轴对称几何模型如图 1b 所示,需要说明的是:基底电极的大小与实际电极不是完全成比例,因为实际基底电极大小为 2 mm,如果完全按比例的话,所需模拟空间过大,造成运算困难,同时也是因为5 倍以上探针大小的基底电极已能产生完整的反馈效应。模拟采用的内置模块为 Transport of DilutedSpecies (tds),具体模拟参数设置,分析与报告结果见 Supporting information。表 1 为 COMSOL 模拟相应的数学模型,结合图 1b 中的标注,表 1 中的边界条件中 1,2 和 3 分别代表探针电极的金属面,周围的玻璃和玻璃斜面;4,8 和 9 代表半无限边界条件,在反应过程中浓度不发生变化;5,6 和 7 代表基底电极的金属面,周围的玻璃和玻璃斜面;10 代表对称轴。根据该数学模型,探针(iT)和基底(iS)电流的积分表达式如下:
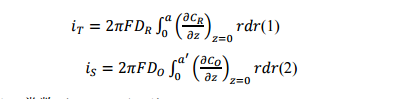
式中,F 为 Faraday 常数(96485 C/mol)。
改变探针与基底电极距离,计算稳态扩散场,并根据式(1)和(2)分别计算探针和基底电极电流,即可获得逼近曲线和收集效率曲线等。
3 结果与讨论
3.1 SECM 反馈效应
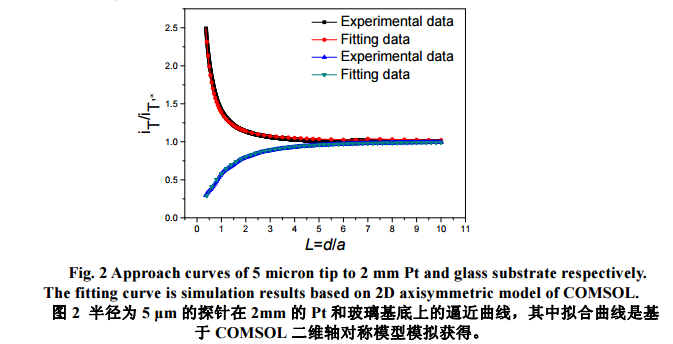
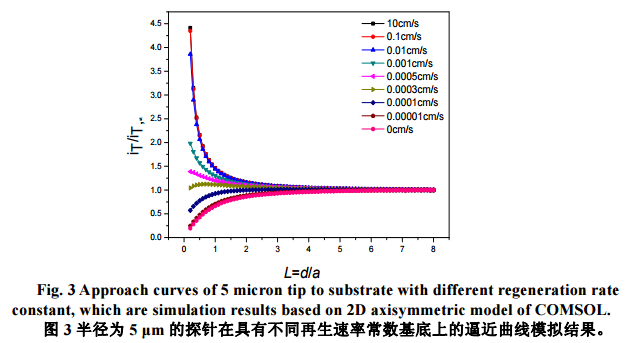
图 2 为直径为 10μm 的 Pt 探针在 2 mm 的 Pt 基底和玻璃基底上的反馈曲线及其对应的模拟曲线结果,其中溶液为 1mmol/L FcMeOH,支持电解质为 0.1 mol/L KNO3 溶液。实验数据显示等效距离 L(L=d/a,d 为探针与基底距离,a 为电极半径)从 10 降至 5 时,归一化探针电流(iT/iT,∞)基本没有明显变化;降至 3,开始出现较为明显的反馈效应;降至 1(探针与基底电极距离为 5μm),正负反馈效应分别为1.42 和 0.71;继续降至 0.5(探针与基底距离 2.5μm),正负反馈效应增强至 2.07 和 0.50。实验数据和拟合结果表明,探针反馈电流与基底性质有关,同时也与探针和基底的距离有关,距离越小,反馈电流效应越强,且正反馈效应大于负反馈效应。这两种反馈效应的基底是 Pt 和玻璃,分别代表 FcMeOH+的还原反应处于扩散控制和反应完全不能发生两种情况。图 3 给出了 FcMeOH+在基底上还原反应不同动力学速率常数下逼近曲线的模拟结果。标准速率常数从 10 cm/s 降至 0.01 cm/s 时,逼近曲线没有明显变化;继续降至 0.0005 cm/s 时,仍保持正反馈,但是与图 2 的正反馈曲线相比较,反馈效应大大减弱;降至 0.0003cm/s,逼近曲线在 L>0.5 时,仍显示正反馈,但进一步逼近基底,电流开始下降(相对于无穷远处,仍是正反馈);降至 0.0001cm/s,出现负反馈;进一步降至 0.00001cm/s 时,与完全负反馈的逼近曲线呈现一致。该结果表明对逼近曲线的反馈行为不仅仅由导体或者绝缘体决定,更为主要的是基底再生动力学的性质,也说明简单通过归一化电流确定探针与基底距离不准确,甚至产生超过 100%的误差,如图中曲线归一化电流均为 1.3 时,动力学速率常数为 0.1,0.001 和 0.0005 cm/s 时对应的距离分别为 6.25,4.5 和 1μm。两组结果都表明,探针与基底距离和基底反应动力学对探针响应电流具有重要影响,也说明精确控制距离对后续 SECM 反馈、产生-收集和动力学计算等实验结果都有影响。
3.2 探针移动距离与真实距离的关系

图 4a 为探针逼近至基底 8μm 处时,每次应用步进马达向基底移动 0.5μm,并在移动结束后通过 CV曲线的平台电流,再根据图 2 的完全反馈曲线上电流确定真实移动距离,而图 4b 则是相反过程,即逐步抬起探针,并监测每个位置下 CV 的平台电流并计算相应归一化电流和距离。如图所示,两组步进马达不同移动方式的移动距离和真实移动距离拟合方程如下:

式中,dreal,a 和,dreal,w 和 dmove 分别为逼近时移动的真实距离,抬起时移动的真实距离和步进马达移动的距离。拟合的结果清楚显示步进马达移动距离与真实距离存在很大差异。两组曲线拟合相关系数高达 0.998,表明真实移动距离与标示移动距离具有良好的线性关系。对于逼近曲线,步进马达显示移动1μm,实际移动距离只有 0.843μm,而对于抬起探针而言,则实际移动距离只有 0.568μm,结果表明通过直接读取步进马达移动距离来确定探针与基底距离会产生很大的误差,而图 2 和图 3 已经显示距离误差对反馈电流具有重要的影响,继而对后续 SECM 实验产生影响。因此在控制距离的 SECM 的实验中,简单通过步进马达移动距离判断探针与基底距离是不准确的,易产生较大误差。
3.3 铝合金表面逼近曲线行为

图 5 为直径 10μm 的 Pt 探针在 0.001 mol/L FcMeOH+0.1 mol/LNaCl 溶液中,逼近 Pt 基底,新鲜ZL104 铝合金表面(抛光后立即浸入溶液进行测试)和自然状态下氧化膜(抛光后自然条件下放置超过24h)的 ZL104 铝合金的归一化电流与距离关系曲线。由图可知,10 μm 的 Pt 探针在 Pt 基底(处于开路状态下)上的逼近曲线呈现完全正反馈特征,与图 1 中的完全正反馈一致,进一步表明 FcMeOH+在金属 Pt 表面的电化学还原反应处于扩散控制,随着探针不断的逼近基底,在基底处反应生成的还原产物扩散至探针表面的距离减小,形成氧化还原循环增加了探针表面的扩散通量,使探针电流随距离 d的减小呈现指数上升的趋势。10 μm 的 Pt 探针在具有自然氧化膜的 ZL104 铝合金基底上的逼近曲线呈现完全负反馈特征,表明在以氧化膜为主的铝合金表面不能发生 FcMeOH+还原反应,随着探针不断的逼近基底,溶液本体中的 FcMeOH+向探针表面的扩散受到抑制,探针表面的扩散通量随 d 的减小而显著降低。相比前两种情况而言,10 μm 的 Pt 探针在新鲜 ZL104 铝合金基底上的逼近曲线所呈现的电流随 d 的减小先增大后减小,表明 FcMeOH+在 ZL104 铝合金的基底还原反应受电荷转移动力学控制,反应速率常数 k0 较小,对比图 2,k0 应接近 0.0003 cm/s。当探针逼近基底时,由于 FcMeOH+形成氧化还原循环增加了探针表面的扩散通量,探针表面的电流呈现增大趋势,但随着探针的不断逼近,FcMeOH+形成氧化还原循环导致的正反馈效应不足以补偿 FcMeOH 扩散受到抑制的负反馈效应,探针电流又出现减小的趋势,称之为不完全正反馈。图 5 结果表明,即使对于同样的铝合金电极基底,由于表面自然状态下氧化膜的状态不同,反馈曲线的类型不同,SECM 测试时不可简单根据完全正反馈或者负反馈判断探针与基底电极距离,而是要建立完整的数学模型,解析出准确距离,否则易判断错误,造成探针撞上基底而破坏探针,以及后续结果分析错误。
3.4 距离对 EC 反应动力学的影响
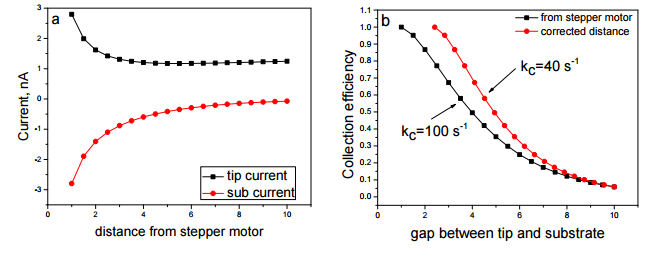


其中,O 为氧化性物种,R 为还原性物种,C 为化学反应产物,电化学反应标准速率常数 k0=1 cm/s,标准电极电位 E0=0 V,传递系数 a=0.5,化学反应速率常数 kc=100 s-1。探针从距离基底 10μm 微米处开始,以 60 nm/s 速度速率,每次移动 0.5μm 微米逐步逼近探针至基底,分别收集探针上还原 O 产生R 的电流和在基底氧化 R 的电流。探针还原电流和基底收集电流,以及收集效率如图 6 所示,根据公式(3)3 和图 4 距离校正后的收集效率曲线也如见图 6b 所示。图 6a 中的探针电流随探针逐渐逼近基底基本保持不变,至 2μm 微米处开始显著增加,表明基底开始大量收集到产物 R,从而形成正反馈,与此同时,基底收集电流在距离为 6μm 微米之前,由于均相化学反应的存在,几乎为 0,随距离减小,基底收集电流逐渐增加。图 6b 显示收集效率(基底电极收集电流/探针电流)随距离减小后逐渐增加,至1μm 微米处接近 100%,表明此时探针产生的 R 能被基底电极完全收集,均相化学反应不能影响基底收集电流。考虑到步进移动距离的校正因素,结合公式(3)3,距离校正后的曲线则表明在距离 2.4μm 微米时,收集效率即可达到 100%,即表明均相化学反应没有标示的 100 s-1 快。建立的 COMSOL 二维模型(见 Supporting information 中的 COMSOL 模型)分别计算探针和基底电流,并计算效应收集效率,表明此时均相化学反应速率常数应为 40 s-1。该结果表明距离计算和控制对于一级均相反应误差可高达60%,也充分说明精确距离控制对于动力学研究的必要性。
4 结 论
(1)正负反馈效应与探针与基底电极距离有关,距离越小,反馈效应越强,同时也与基底电极再生动力学有关。步进马达控制的探针逼近和离开基底电极移动距离与探针真实移动距离的比例是 0.843和 0.568,即步进马达标示移动 1μm,而实际仅有 0.843 和 0.568μm,因此控制探针距离须严格按照计算归一化电流,并结合反应模型来量化。
(2)铝合金表面氧化膜的状态影响逼近曲线行为,从部分正反馈至完全负反馈,而步进马达移动引入的距离误差导致 EC 反应中一级化学均相反应的动力学速率常数误差高达 60%。
(3)严格控制并明确距离是扫描电化学显微镜实验的基础,也是后续分析的前提。