唐云涛 刘子莲 左新浪 工业和信息化部电子第五研究所
目前,针对碳钢在潮湿环境中的可靠性分析中,主要通过结构件腐蚀深度模型来计算结构件在服役期间内的厚度均值和方差,然后根据均值和方差来判断结构件的强度是否符合现阶段的设计要求,因此合理的腐蚀模型是该方法的首要任务。碳钢在潮湿的环境中可能会发生全面腐蚀或者局部腐蚀,现已有大量的腐蚀模型被提出。
1 全面腐蚀模型
现有的全面腐蚀模型大致可以分为两类:经验模型和物理模型,经验模型主要是基于结构件在潮湿环境中的实际测量数据,然后通过实际的方法拟合出曲线,物理模型主要是基于腐蚀涉及到的物理学原理推导得出[1-2] 。
1.1经验模型
早些年间,科学家们假定腐蚀具有恒定的腐蚀速率,不同阶段的腐蚀速率不同,据此,1979 年,Southwell [3] 等提出了线性以及双线性模型,通过目前学者的腐蚀研究数据可知,线性模型不能准确的解释结构件在实际服役环境中的发生的腐蚀行为,更不能预测后期腐蚀深度。1998 年 Paik 等[1-2]采用统计学方法将腐蚀模型划分为两个阶段:腐蚀防护系统有效阶段和腐蚀发生阶段,为了便于分析假定腐蚀发生在腐蚀防护系统失效以后,同时 Paik 等假定耐蚀涂层寿命服从正态分布,假定耐蚀涂层失效后的腐蚀速率与腐蚀时间呈现幂函数关系,Paik 的腐蚀模型如图 1 所示,图中 t τ 为腐蚀深度,T 为结构件的服役时间,Tc 为耐蚀涂层的寿命,Tt 为过渡时间,C 1 和 C 2 为系数,该腐蚀模型幂指数的大小可以模拟出不同的腐蚀过程,当幂指数大于 1 时,腐蚀模型为 C,腐蚀速度不断加快,可以模拟腐蚀产物不断被清理的过程;当幂指数等于 1 时,腐蚀模型为 B,即为恒定腐蚀速率;当幂指数小于 1 时,腐蚀模型为 A,表明腐蚀速率不断降低,可以模拟腐蚀产物不断堆积的过程。
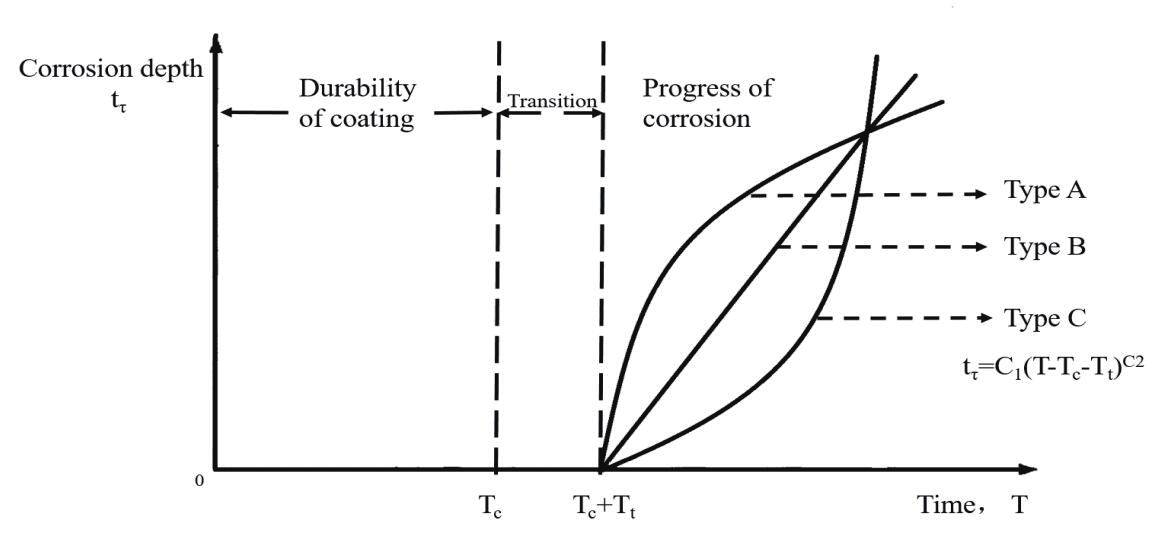
图1 Paik腐蚀模型
1999 年,Guedes Soares 和 Garbatov [4] 提出了非线性腐蚀模型,该模型与 Paik 的模型相一致,主要描述了腐蚀过程的三个阶段,分别是耐蚀涂层保护有效过程、耐蚀涂层发生破坏,腐蚀深度非线性增长过程和腐蚀产物减缓了腐蚀速率的过程。根据上述三个腐蚀阶段的假定,Guedes Soares 和Garbatov 假设耐蚀涂层的寿命服从统计学上的正态分布,提出了一个腐蚀模型,该模型的形式为指数函数,并成功的运用该模型描述了货轮侧板在海洋潮湿环境下的腐蚀过程。上文中提到的指数函数腐蚀模型和幂函数腐蚀模型数学形式较为简单,应用方便,但他们均认为腐蚀发生在耐蚀涂层失效以后,而没有认识到腐蚀与耐蚀涂层失效是同时发生的。2003 年,秦圣平和崔维成[5]提出了可靠性分析中常用的 Weibull 函数形式的腐蚀深度概率模型,该函数不仅应用在腐蚀领域,也应用在其他模式失效的领域,具有相当广范围的应用性。Weibull 模型能够同时描述结构件腐蚀过程的加速和减速阶段,更符合实际应用中的腐蚀情况。
上述的腐蚀模型虽然具有较强的应用价值,但经验模型需要通过大量的实验进行数据收集,并对模型进行校正,且应用模式较为单一,在同一腐蚀环境收集的数据只能应用在当前环境,无法对另一腐蚀环境进行预测。
1.2物理模型
物理模型以腐蚀过程中的热力学、离子扩散理论等为基础,在上世纪六十年代,Evans [6] 等认为铁离子的迁移为腐蚀过程中的主要控制因素。九十年代左右 Chernov [7] 等认为氧在腐蚀介质中的扩散速度是腐蚀过程中的主要控制因素,同时,他们还综合考虑了温度,氯离子浓度等其他因素的影响。
近现代,Melchers [8] 提出了一个概念性腐蚀模型,模型示意图如图 2 所示,该模型也称为“多阶段现象学腐蚀模型”。该模型描述了无耐蚀涂层下碳钢等结构件在潮湿环境中的全面腐蚀过程,该模型将腐蚀过程分为四个阶段:(1)初始腐蚀阶段;(2)腐蚀产物生长所导致的氧气扩散控制阶段;(3)有氧活动控制阶段;(4)厌氧活动控制阶段。Melchers 通过大量实验结果表明:在初始腐蚀阶段,腐蚀速率保持稳定,在氧气扩散控制阶段,腐蚀速率随着时间呈现出非线性变化,即在该阶段刚开始时速率大,而后逐渐减小,在有氧活动和厌氧活动控制阶段,腐蚀速率与腐蚀时间呈现出幂函数的变化规律,并且该阶段的腐蚀状态与腐蚀环境的氧气扩散呈现出比例关系。“多阶段现象学腐蚀模型”是近年来代表性的创作之一,他能够简洁明了的指出结构件在潮湿环境中的腐蚀规律,但它也具有一定的缺陷,即仅适用于没有耐蚀涂层并且发生全面腐蚀的结构件,而且其实用性不强,因此,现阶段还很难将其应用。
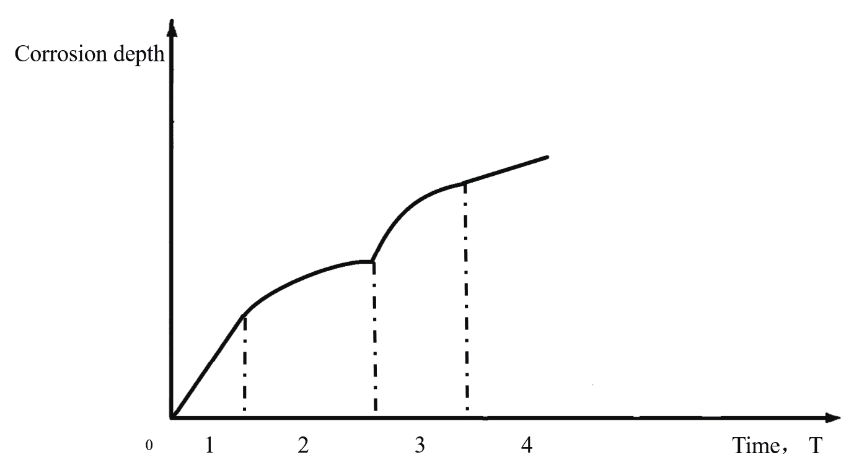
图2 多阶段现象学腐蚀模型
2 局部腐蚀模型
现阶段对于局部腐蚀的研究对象集中在点蚀方面,且模型也不成熟,处于初级阶段,目前科研人员认为点蚀腐蚀坑深度与腐蚀时间的关系呈现为幂函数的形式,如下式1所示。式中 d(t) 式点蚀坑的深度,t 是暴露时间,ti 是点蚀发生的时间,c1 和 c2 是待定系数。
d(t)c1(t-ti)c2,t ≥ ti (式 1)
式 1 的模型主要适用于短期腐蚀,而在长期腐蚀中的应用存在较大偏差,也有学者认为该短期腐蚀模型是由于厌氧环境引起的。
2003年,Paik等[1-2] 学者通过统计学分析后,提出了式2,并认为该模型可以用于描述结构件在潮湿环境中的局部腐蚀行为,式 2 中,Tc 是耐蚀涂层寿命,并假设其服从对数正态分布,d(t) 是腐蚀速率,为随机变量,且服从 Weibull分布。该模型虽然在实际应用中存在一定的借鉴意义,但是无法解释腐蚀过程的相关理论。
d(t)c1(t-Tc),t≥Tc (式2)
2005 年 Melchers [8] 将点蚀坑深度服从 Gumbel 分布,而且结合全面腐蚀模型中的多阶段现象学模型建立了碳钢在潮湿环境中的最大点蚀坑深概率模型,如图 3 所示,该模型也称为点蚀现象学腐蚀模型,模型一共分为 5 个阶段:第 0阶段用于点蚀微观层面的描述,点蚀初始时腐蚀速率迅速增大,此时腐蚀速率主要取决于碳钢表面是否有涂层以及腐蚀环境的恶劣程度;第 1 阶段取决于活化控制的情况,腐蚀环境中的氧的扩散速率起到了关键作用;第 2、3 和 4 阶段用于描述宏观点蚀,第2 阶段时,潮湿环境中的氧气溶解扩散速率在腐蚀产物影响下会发生较大的变化,此时腐蚀产物起到了关键性作用;第 3 阶段和第 4 阶段表明在厌氧控制下,点蚀坑深缓慢增长。该点蚀模型具有较高的可信度,但是,它也有一定的缺陷性,比如,模型参数多,模型阶段性较多,在运用的过程中较难判断点蚀坑位于哪一阶段,参数也需要大量数据推算。
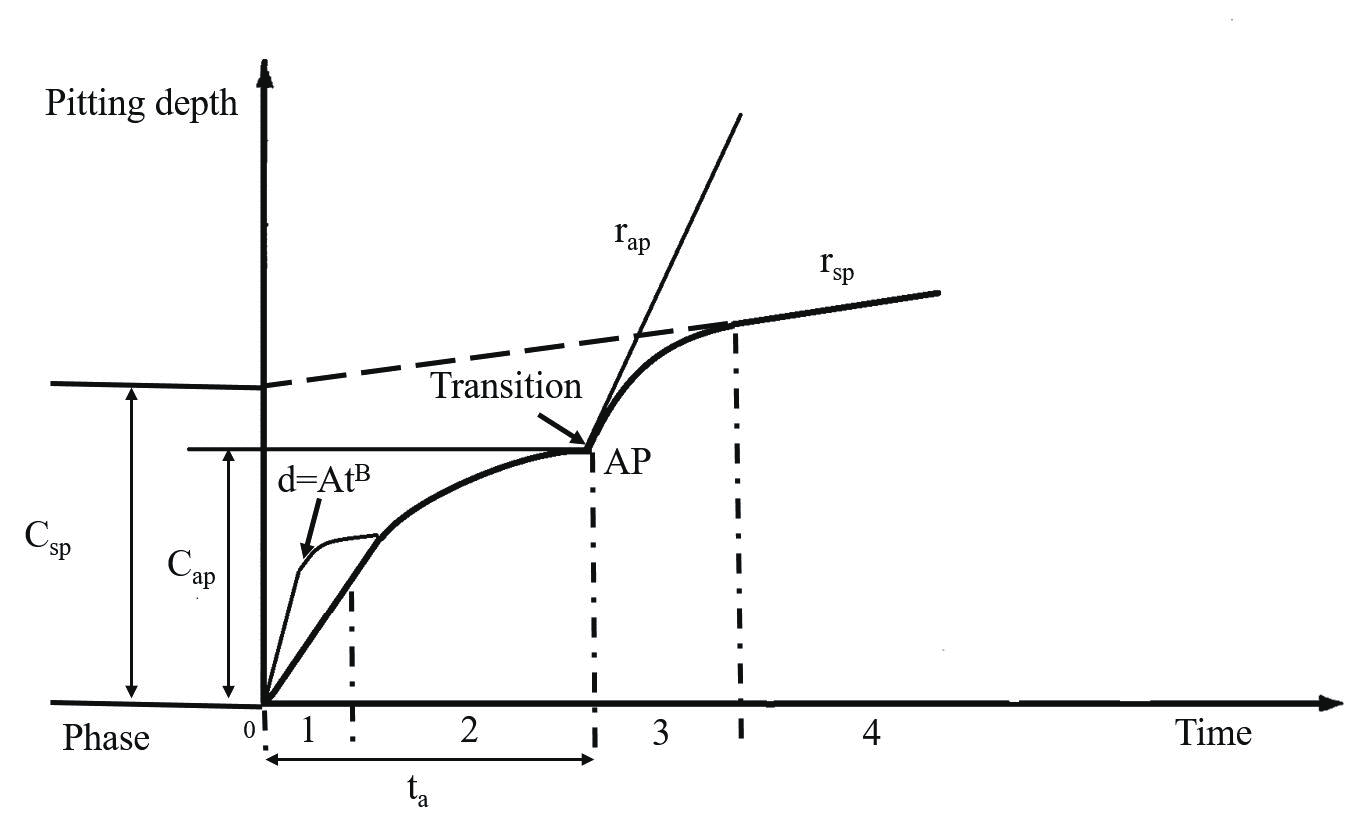
图3 点蚀现象学腐蚀模型及参数
在全面腐蚀模型中,应用较为广泛的属于 Weibull 模型,在点蚀模型中,Weibull 模型也依然适用,2008 年,王燕舞[9]提出了适用 Weibull 函数来描述点蚀坑深与腐蚀时间的关系,如式 3 所示,式中,dm 是点蚀坑深度最大值,Ti 是点蚀坑发生的时间,α 和 m 是待定系数。在实际应用过程中,该模型参数为随机变量,可以通过大量的实验数据可以获得参数的数值和方差。相比较于传统的模型,该模型更为直接清楚的描述点蚀坑深随着时间变化的规律,此外,该模型参数较少,较为容易确定。但该模型与其他的经验模型一样,无法对点蚀坑的微观腐蚀机理进行研究,具有一定的不足。
d(t)dm{1-exp[-α(t-Ti )m]},t ≥ Tc (式 3)
4 结论
通过总结前人提出的大量腐蚀模型可知现阶段腐蚀模型研究主要以全面腐蚀为主,且全面腐蚀已经积累了较多的数据,而点蚀模型由于影响因素较多,点蚀坑实测难度比全面腐蚀大,缺乏比较完整的点蚀数据库,因此点蚀模型尚处于研究论证阶段。但无论是全面腐蚀还是局部腐蚀,统计学方法均可以对其进行相关的预测,因此通过统计学对腐蚀寿命进行预测将来是重点的发展方向,但同时也需要相关科研人员完善腐蚀机理研究以便更好地应用模型。
参考文献 :
[1] Paik J K, Thayamballi A K. Ship-shapedoffshore installations: design, building, andoperation. New York: Cambridge University Press,2007.
[2] Paik J K, Kim D K. Advanced method for thedevelopment of an empirical model to predict time-dependent corrosion wastage. Corrosion Science,2012,63:51-58.
[3] Southwell C R, Bultman J D, Hummer CW. Estimating service life of steel in seawater.In:Schumacher M, editor. Seawater CorrosionHandbook. New Jersey: Noyes Data Corporation,1979:374-387.
[4] Soares C G. Garbatov Y. Reliability ofmaintained, corrosion protected plates subjected tonon-linear corrosion and compressive loads. MarineStructures, 1999,12(6)425-445.
[5] Qin S P, Cui W C. Effect of corrosion modelson the time-dependent reliability of steel platedelements, Marine Structures, 2003, 16(1):15-34.
[6] Evans U R. The corrosion and oxidation ofmetals: scientific principles and practical application,London: Edward Arnold, 1960.
[7] Chernov B B, Ponomarenko S A.Physicochemical modelling of metal corrosion inseawater. Protection of Metals, 1991, 27(5):612-615.
[8] Melchers R E. Modeling of marine immersioncorrosion for mild and low-alloy steels-part 1:phenomenological model. Corrosion, 2003,59(4):319-334.
[9] Wang Y W. Study on the ultimate strength ofship structure considering corrosion [Dissertation].Shanghai: Shanghai Jiaotong University, 2008( 王燕舞 . 考虑腐蚀影响船舶结构极限强度研究 [ 学位论文 ]. 上海:上海交通大学,2008)